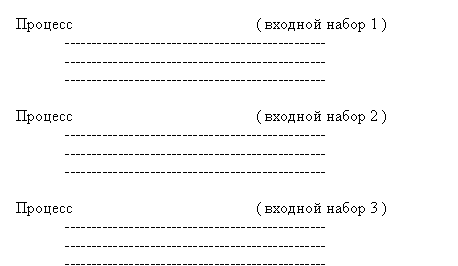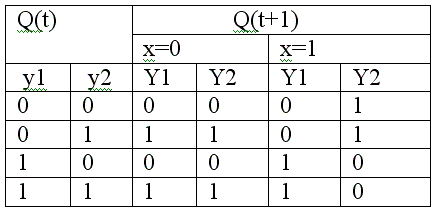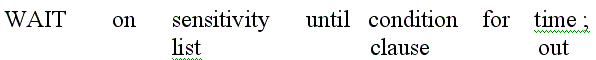3 Базовые методы моделирования
В настоящей книге будут рассматриваться преимущественно модели уровня СБИС.
Однако все подобные модели обязательно содержат элементы базовых моделей комбинационных и
последовательностных схем. В данной главе мы объясним, каким образом разрабатывать такие базовые модели.
Моделирование параллельности
К моделированию логических схем предъявляются требования,
которые не характерны для многих других применений методов и средств моделирования:
речь идет о том, что модель должна предусматривать параллельное выполнение.
Это обусловлено тем, что логические сигна-лы передаются и обрабатываются параллельно.
Иллюстрацией этого понятия может служить схема рис. 3.1.
Здесь показаны три логических блока. Если предположить, что входной набор 1 и входной набор 2 активируются
одновременно, то логические блоки 1 и 2 будут акти-вироваться также одновременно.
Логический блок 3 будет активироваться, как только произойдет изменение значения на выходе логического
блока 1 (Z1) или логического блока 2 (Z2).
Когда эти сигналы проходят через логический блок 3, через блоки 1 и 2 могут проходить новые
измененные значения входных сигналов. Таким образом, поток сигналов может проходить через все блоки одновременно.
Язык описания аппаратуры должен иметь средства для отображения такой одновременности.
В языке VHDL это требование реализуется при помощи механизма процессов.
Каждый процесс представляет некоторый логический блок моделируемой схемы,
причем все процессы выполняются параллельно.
(Если система моделирования работает на одном процессоре, то, естественно,
фактически они будут выполняться последовательно, однако с точки зрения моделирования
это будет выглядеть так, как если бы они выполнялись параллельно.) В языке VHDL процесс активируется,
когда происходит изменение какого-либо сигнала в списке сигналов запуска этого процесса.
На рис. 3.2 показаны структуры процессов языка VHDL, соответствующие структуре логических блоков рис. 3.1.
Отметим, что список сигналов запуска данного процесса в общем случае
содержит входной набор сигналов соответствующего логического блока.
В качестве конкретного примера укажем, что ло-гический блок 1 может быть представлен
процессом, приведенным на рис. 3.3.
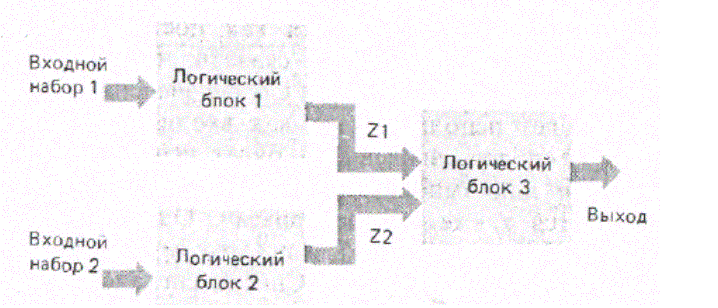
рис. 3.1 Структура с логическими блоками
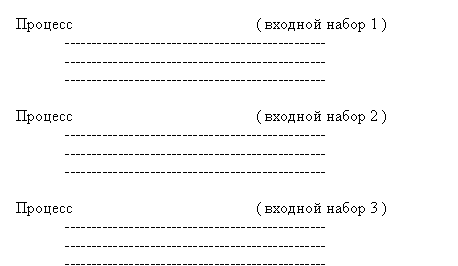
рис. 3.2 Три параллельных процесса

рис. 3.3 Пример процесса (для логического блока 1)
Отметим, что на рис. 3.3 тело процесса содержит вначале раздет описаний, где объявляется переменная Y1NT, которая является ло-кальной для процесса. Выполняемый раздел (между ключевыми словами begin и end) содержит оператор присваивания переменной, который
вычисляет промежуточное значение (Y1NT) и за которым следует опе-ратор назначения сигнала, завершающий выполнение функции и учиты-вающий задержку распространения сигнала в блоке.
Концепция процесса может быть также реализована в базовых операторах регистровых передач. Рассмотрим следующие два оператора регистровых передач:
A = X * Y ; - оператор S1.
B = A + Z ; - оператор S2.
Поскольку эти операторы печатаются как последовательный текст, первая и естественная наша реакция-сказать, что они выполняются последовательно. Отметим, что в этом случае значение А. вычисленное оператором S1, будет использоваться как входное для оператора S2; другими словами, новое значение А будет использоваться как фак-тический параметр для выполнения S2. Такое последовательное вы-полнение называется также процедурным . Однако показанные два оператора можно интерпретировать и по-другому. Операторы S1 и S2 можно рассматривать как процессы. Список сигналов запуска для S1 содержит X и Y, а для S2-А и Z. Однако, прежде чем приступить к анализу выполнения S1 и S2 как процессов, необходимо обсудить еще одно понятие, касающееся процесса. Поскольку процесс представляет физическую систему, время его выполнения не может быть нулевым. Пример на рис. 3.3 показывает, каким образом процессу может быть присвоено значение задержки распространения. При этом, если такое значение не указано, мы говорим, что процесс выполняется за время дельта , бесконечно малое, но большее нуля. Обсудим теперь вы-полнение S1 и S2, если их рассматривать как процессы. Предположим, что значения X и Z меняются одновременно в момент времени t1. При этом активируются и S1, и S2. Отметим, однако, что в этом случае значение А, используемое в операторе S2, будет относиться к моменту t1 и определяться значениями X и Y момента времени (t1-дельта). Новое значение А появится в момент (t1 + дельта), и, если это значение отражает изменение А, в этот момент произойдет активация S2.
Проиллюстрируем это на примере рис. 3.4 (а). Предположим, что все сигналы этой таблицы относятся к целому типу. Напомним, что знаки * и + обозначают операции целочисленного умножения и сложения соответственно. В момент времени (t1- дельта) значения А и В не-известны (u), поскольку неизвестны предыдущие значения X, Y и Z. В момент t1 значение А определяется значениями X и Y момента (t1- дельта); на этом значении не отражаются изменения X, происходящие в момент t1. Это изменение X в момент t1 скажется на значении А момента (t1 + дельта) и значении В момента (t1 + 2*дельта).
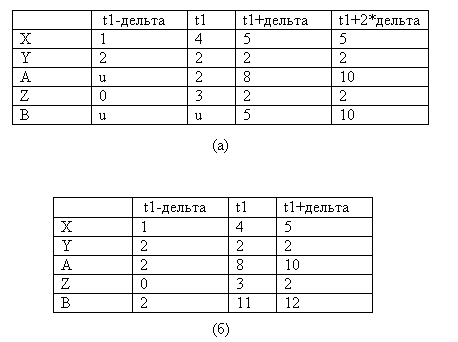
рис. 3.4 а- интерпретация S1 и S2 как процессов; б- процедурная интерпретация S1 и S2.
На рис. 3.4,6 показан случай, когда операторы S1 и S2 выполняютс* процедурным образом (т. е. последовательно). Отметим, что в этом случае результат изменений сказывается немедленно (т. е. без задержка величиной дельта).
Возвращаясь к интерпретации операторов как процессов, мы должны дать ответ на следующий принципиальный вопрос: Что представляет собой дельта? . Правомерный ответ-что дельта есть один цикл прогона модели. В принципе, имитационная модель состоит из множестве процессов. Во время прогона модели в данном цикле запускаются ва процессы, входные параметры которых изменились с момента вы полнения последнего цикла. Предполагается, что выходные сигналь этих процессов будут действовать в более поздние моменты времен! моделирования. После того как все процессы выполнены, данный цию моделирования считается завершенным, Следующий цикл начнется нос ле того, как в очередной раз произойдет изменение какого-то входной сигнала для какого-то процесса. Этот период может составлять нано секунды времени моделирования или он может просто означать, что мь перешли на следующий цикл моделирования (т. е. сделали временно шаг величиной дельта). Шаг величиной дельта образуется при вы-полнении операторов назначения сигналов, например S1 и S2, не имею-щих фразы after.
С точки зрения логической схемы дельта-это задержка на одном уровне-каскаде логики. Операторы S1 и S2 представляют модель потока данных , а механизм дельта-задержек дает возможность имиировать задержку сигналов на модели, не задавая конкретных значений распространения.
Проблема последовательного или параллельного выполнения на-ходит также свое отражение в типе объектов, используемых в опера-торах регистровых передач. Для иллюстрации рассмотрим снова при-веденный выше пример с операторами S1 и S2. Если мы предполагаем, что эти операторы выполняются последовательно, то, согласно при-нятой в языке VHDL терминологии, А есть переменная в том смысле, что она не имеет временной размерности (т.е. она немедленно при-присваиваемое ей значение). Если предполагается параллельное операторов, то А-это сигнал , значение которого может измениться только через некоторый конечный промежуток времени (минимум дельта) после соответствующего присваивания.
Поскольку в общем случае по тексту программы нельзя определить, предполагается ли последовательное или параллельное выполнение операторов, необходимо либо при помощи специальной нотации, либо семантики конкретного языка указать, какой режим выполнения в виду. В языке VHDL для этой цели служит специальная Параллельное выполнение операторов указывается при помощи сим-вола < =. а символ : = обозначает процедурное выполнение. Таким образом, если бы для приведенного выше примера предполагалось параллельное выполнение, следовало бы написать его следующим об-разом:
А < = X * Y; оператор S1
В < = А + Z; оператор S2.
Здесь оба оператора называются операторами назначения сигнала. В случае процедурного выполнения пример нужно было бы написать так:
А: = X * Y; оператор S1
В: = А + Z; оператор S2,
где оба оператора называются операторами присваивания переменной. Требует ответа еще один важный вопрос: где в описаниях на языке VHDL могут быть использованы операторы присваивания для пе-ременных и сигналов? Операторы присваивания значений переменным разрешается использовать внутри процессов (рис. 2.2 и 3.3) и в под-программах (функциях или процедурах). На рис. 2.12 приведен пример их использования в подпрограмме. С другой стороны, оператор на-значения сигнала подразумевает процесс и поэтому может встречаться в месте выполняемого раздела архитектурного тела. Существует ситуация, которая несколько затуманивает такую картину. Опе-раторы назначения сигналов могут также встречаться в блоке процесса. Именно это показано на рис. 2.2 и 3.3; приведем еще один пример, лучше иллюстрирующий подобную ситуацию:
process(R.S)
begin
A <= X*Y; oneparop S1
B <= A+Z; oneparop S2
end process;
Этот пример интерпретируется следующим образом. Выполнение опе-раторов S1 и S2 не начинается по изменениям значений X, Y, Z. или А. Для данного блока процесса в список сигналов запуска входят R и S. Таким образом, когда произойдет изменение R или S, операторы S1 и S2 выполнятся параллельно. В правых частях этих операторов будут использоваться текущие значения X, Y, Z. и А, на основе которых вычислены значения А и В для момента времени через один шаг льта. На использование операторов назначения сигналов в процессов накладывается только одно ограничение: можно опрс-только по одному драйверу на сигнал в процессе. Таким образом, если в рамках одного и того же процесса имеются два оператора для одного и того же сигнала, разработчик модели должен возможные последствия наложения одного значения сигнала на другой,-поскольку функция разрешения шины здесь не предусматри-вается. Однако, как увидим из последующих примеров моделирования обычно это не создает особых проблем - ввиду принятой методологии написания моделей.
Следует иметь в виду, что природа оператора назначения сигнала, оператора присваивания переменной и блоков процессов дает разра-ботчику моделей ряд возможностей выбора. В начале проектирования разработчик может использовать блок процесса, алгоритм которого реализуется при помощи операторов присваивания переменных, а по-следний оператор блока есть оператор назначения сигнала, вычисляю-щий выходной сигнал блока. Такой подход иллюстрируется рис. 2.2 и является достаточно эффективным, поскольку не ориентируется на конкретную аппаратную структуру. Другой подход заключается в том, чтобы использовать операторы назначения сигналов, подход, называемый иногда реализацией потока данных , показан не рис. 2.4. Он ориентирован на конкретную аппаратную структуру и поэтому более целесообразен для последних этапов проектирования.
Моделирование комбинационной логики
В этом разделе мы опишем базовые методы моделирования ком-бинационной логики. На рис. 3.5 показана подобная схема в общем виде: входной вектор X поступает на комбинационную логическую схему CL, на выходе которой получается вектор F. Схема считается чисто ком-бинационной, если в ней нет обратных связей или механизмов хранения заряда, т.е. элементов памяти. Для иллюстрации базовых методов моделирования рассмотрим простой случай комбинационной схемы с одной выходной функцией F = XI *Х2 + ХЗ.

рис. 3.5 Базовая модель комбинационной логической схемы (CL).
На языке VHDL простая модель этой функции имеет вид:
entity CL is
port(X1,X2,X3: in BIT;
F: out BIT);
end CL;
DATA_FLOW of CL is
signal T1: BIT;
begin
T1 <= X1 and X2;
F <= T1 or X3;
end DATA_FLOW;
Оба оператора этой модели выполняются параллельно, поэтому модель является моделью потока данных и представляет схему уровня ло-гических вентилей, показанную на рис. 3.6. Задержка на каждом ло-гическом вентиле -произвольно малая величина времени дельта, ко-торая обсуждалась выше. Если разработчик желает моделировать за-держки более точно, он может использовать следующие две последо-вательности операторов:
T1 <= X1 and X2 after DEL1;
F <= T1 or X3 after DEL2;
В данном случае мы назначаем конкретные задержки распространения для каждого из конкретных логических вентилей. Значения задержек DEL1 и DEL2 необходимо задавать при помощи константы, выражения или объявленного параметра настройки. Мы проиллюстрируем эти способы в гл. 4.
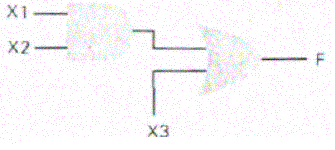
рис. 3.6 Cхема уровня логических вентелей для реализации функции F
Альтернативное представление содержимого блока в случае исполь-зования механизма процессов может быть следующим:
architecture PROCESS_lMPL of CL is
begin
process (X1.X2.X3)
variable T1: BIT;
begin
T1 := X1 and X2;
F <= T1 or X3 after TOTAL_DEL;
end process;
end PROCESSJMPL;
В этом случае активация процесса происходит каждый раз, когда меняет свое значение любой сигнал, входящий в его список сигналов запуска (XI, Х2, ХЗ). После активации процесса оба его оператора выполняются последовательно. Здесь Т1-переменная, значение которой обновляется немедленно (т. е, в данный момент времени моделирования, без дель-та-задержки). Затем выполняется второй оператор, и значение F под-готавливается к изменению после приращения времени на величину
общей задержки ТОТАL_DEL.
Если не считать того факта, что этот подход позволяет нам моде-лировать общую задержку вместо индивидуальных задержек, как в модели потока данных, на первый взгляд у него практически нет преимуществ по отношению к механизму процессов. Рассмотрим, од-нако, следующую альтернативную реализацию блока процесса в том же самом архитектурном теле:
ROM: process(X1.X2.X3)
type FUNC_VALUES is array(0 to 7) of BIT;
variable MEM: FUNC_VALUES:="01010111";
begin
F <= MEM(INTVAL(X1&X2&X3))after TOTAL_DEL;
end process ROM;
Приведенная реализация подразумевает представление логической функ-ции ПЗУ (RОМ). Здесь ПЗУ моделируется при помощи одномерного
массива типа FUNC_VALUES (значения функции), определяющего
битовый вектор длиной 8. Описание переменной определяет этот тип для переменной памяти МЕМ и инициирует МЕМ выходными значениями функции. МЕМ-одномерный массив с целочисленным индексом. Для доступа к этому массиву производится конка гснация трех входных параметров, XI, Х2 и ХЗ, с преобразованием в тип INTEGER при помощи функции INTVAL (VECT), которая осуществляет преобразо-вание битового вектора в тип INTEGER. Реализация этой функции описана в гл. 5. Подход с использованием ПЗУ для реализации ком-бинационной логики отличается исключительной гибкостью, поскольку для изменения логики необходимо только изменить инициализацию переменной. Такой же подход может быть принят при реализации логических функций с использованием микросхем программируемых логических матриц (ПЛМ, PLA) и программируемой матричной логики (ПМЛ, PAL). Рассмотрим еще один способ реализации комбинационной логики-при помощи мультиплексора МУX:
MUX: process (X1,X2,X3)
begin
case X1&X2&X3 is
when "000" => f <= '0' after TOTAL_DEL;
when "001" => f <= '1' after TOTAL_DEL;
when "010" => f <= '0' after TOTAL_DEL;
when "011" => f <= '1' after TOTAL_DEL;
when "100" => f <= '0' after TOTAL_DEL;
when "101" => f <= '1' after TOTAL_DEL;
when "110" => f <= '0' after TOTAL_DEL;
when "111" => f <= '1' after TOTAL_DEL;
end case;
end process MUX;
В этом варианте реализации сочетание логических единиц и нулей (т.е. значений f) является выходом мультиплексора. Конкретное значение f выбирается по состояниям управляющих входов XI, Х2 и ХЗ.
В языке VHDL существует оператор назначения сигнала с выбором, позволяющий получить несколько более сжатую реализацию с исполь-зованием мультиплексора:
with X1&X2&X3 select
f<= '0'after TOTAL_DEL when "000";
'1'after TOTAL_DEL when "001";
'0'after TOTAL_DEL when "010";
'1'after TOTAL_DEL when "011";
'0'after TOTAL_DEL when "100";
'1'after TOTAL_DEL when "101";
'0'after TOTAL_DEL when "110";
'1'after TOTAL_DEL when "111";
В приведенном примере оператор назначения сигнала с выбором просто заменяет оператор-процесс в архитектурном теле.
Моделирование последовательностной логики
В предыдущем разделе мы определили комбинационную логическую схему как схему, не имеющую кошуров обратной связи или элементов памяти. А схемы, в которых эти цепи и элементы присутствуют, называются последователъностными. Последовал ельностные схемы мо-гут быть представлены моделью Хаффмана, которая показана на рис. 3.7. Базовые компоненты этой модели-блок комбинационной ло-гики и множество контуров обратной связи. На вход блока ком-бинационной логики поступают внешний входной вектор X и текущее значение состояния схемы YDEL. Выходы блока это выход схемы 2 и следующее значение переменных состояния Y. Задержка DEL может быть либо "тактированной (синхронной), либо чистой задержкой рас-пространения (асинхронной). Рассмотрим вначале пример с синхронной задержкой. На рис. 3.8, показана структурная схема модуля прямого счетчика. Когда на входе управления СОN логическая 1, счетчик считает в прямом направлении с частотой 2 МГц. а когда логический О, состояние счетчика не меняется.
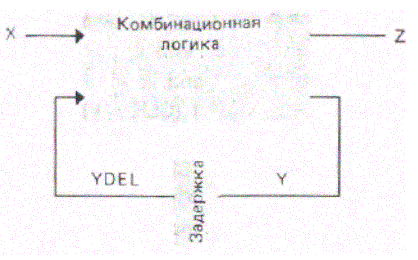
рис. 3.7 Модель Хаффмана для последовательностной схемы
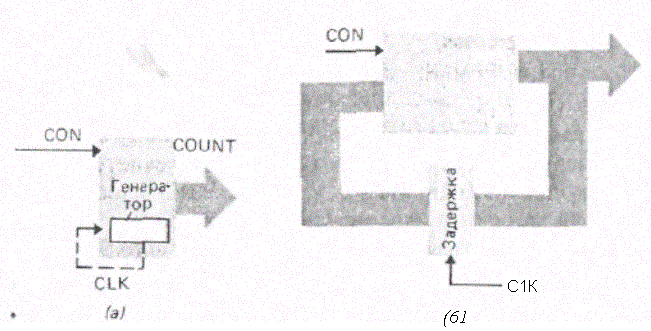
рис. 3.8 Модель Хаффмана для схемы прямого счетчика: а- прямой счетчик; б- модель Хафмана
На рис. 3.8, показана модель Хаффмана для этого счетчика. Блок комбинационной логики счетчика-это инкрементор, разрешением для которого служит входной управляющий сигнал СОN. Задержка об-ратной связи реализуется при помощи тактированных триггеров. Функ-цию инкрементора можно описать при помощи модели комбинационной логики, описанной выше. Полная модель счетчика, которую разработал Донгал Хан, выглядит следующим образом:
entity COUNTER
port(CON: in BIT;
Z: out BIT_VECTOR(0 to 3});
generic(CLOCK_WIDTH,COUNT_DEL);
end COUNTER;
use INC.all;
architecture HUFFMAN of COUNTER is
signal CLK: BIT:= '0';
begin
process(CON.CLK)
variable COUNT: BIT_VECTOR{0 to 3):= "0000";
begin
if not CON'STABLE then
if CON = T then
CLK <= transport '1' after CLOCK_W!DTH;
else
CLK <= transport '0';
end if;
end if;
if ((CLK ='1') and not CLK'STABLE) then
COUNT := INC(COUNT);
CLK <= transport '0' after CLOCK_WIDTH/2;
CLK <= transport '1' after CLOCK_WIDTH;
end if;
Z <= COUNT after COUNT_DEL;
end process;
end HUFFMAN;
Модель представляет последовательностную природу счетчика двояким образом. Во-первых, состояние счетчика отображается в переменной СOUNT. Поскольку все процессы в языке VHDL живут в течение периода прогона модели, значение, зафиксированное в этой переменной счетчика, будет сохраняться. Во-вторых, функция синхронизации, реали-зуемая встроенным генератором счетчика, моделируется путем задер-жанного присваивания значений '0' и '1' сигналу СLK с учетом того факта, что изменение СLK будет активировать процесс, вырабатываю-щий этот сигнал. Таким образом представляется механизм задержанной обратной связи модели Хаффмана. Отметим, что генератор запускается положительным фронтом сигнала СОN и отключается по отрицатель ному фронту этого сигнала. Наконец, оператор назначения синхро сигнала СLК содержит ключевое слово transport (транспорт). Так еде лано для того, чтобы один оператор присваивания не накладывался ш другой. Более ясно это станет после прочтения гл. 4, где мы обсуждаел-понятие инерционной и транспортной задержек.
Аналогичным образом могут быть описаны асинхронные схемы причем механизм процессов предусматривает возможность гибко ука зывать уровень, на котором моделируется схема. Рассмотрим следук> щую таблицу потоков сигналов для конкретной асинхронной последова-тельностной схемы:
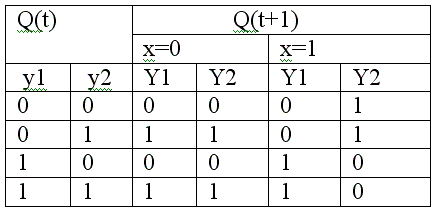
Первоначально разработчику модели, быть может, не нужно указы-вать физическую реализацию схемы. Приведем модель на языке VHDL где таблица потоков сигналов хранится в виде массива АRRAY:
entity ASYNC is
port(X : in BIT;
Y1.Y2: inout BIT);
end ASYNC;
use INTVALall
architecture ROM of ASYNC is
type SQ_ARRAY is array(0 to 7, 0 to 1) of BIT;
variable MEM: SQ_ARRAY:=(('0','0'),('1','1'),('0','0'),
('1','1'),('0','1'),('0','1'),
('1','0'),('1','0'));
begin
process(X,Y1,Y2)
begin
Y1 <= MEM(INTVAL(X&Y1&Y2),0) after PROP_DEL;
Y2 <= MEM(INTVAL(X&Y1SY2),1) after PROP_DEL;
end process;
end ROM;
При обращении к массиву первый индекс вычисляется путем кон-катенации X, Y1 и Y2 с последующим преобразованием этого трех-элементного битового вектора в тип INTEGER. Отметим, что выводы YI и Y2 описаны в интерфейсе как двунаправленные (inout). Это дает возможность обращаться к ним при помощи одиночных операторов-процессов в архитектурном теле, а также управлять ими через эти процессы.
По мере проектирования схемы для переменных состояния Y1 и Y2 разрабатываются логические формулы:
Y1 = х* у2 + х*y1
Y2 = x* у2 + х*у1, курсивное, полужирное начертание = НЕ
Альтернативный подход к моделированию схемы на этом этапе проек-тирования может быть представлен следующим архитектурным телом
architecture GATE_LEVEL of ASYNC is
begin
Y1 <= (not X and Y2) or (X and Y1) after DEL1;
Y2 <= (not X and Y2) or (X and not Y1) after DEL2;
end GATE_LEVEL;
Приведенные выше примеры свидетельствуют о том, что механизм обратных связей моделируется одинаково для синхронных и асинхрон-ных схем. Меняется только семантика переменной обратной связи: для синхронных схем переменная обратной связи представляет период так-товой частоты, а для асинхронных схем-задержку распространения.
Поведение тактированного триггера
Еще одна важная характеристика последовательностных схем, тре-бующая представления в модели,-это поведение тактированного триг-гера. На рис. 3.9 показана блок-схема триггера-защелки типа D.
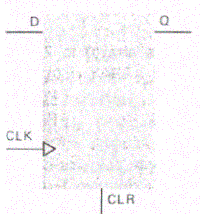
рис. 3.9 Триггер-защелка типа D
Когда на входе синхронизации СLК высокий уровень, выходной сигнал Q повторяет входной сигнал D; когда вход синхросигнала СLК пере-ключается в низкий уровень, текущее значение Q защелкивается . При низком уровне СLК хранящееся значение Q не меняется. Триггер-защелка имеет также вход асинхронного сброса СLR. Если на этот вход подать сигнал 1, триггер сбрасывается. Асинхронный сброс имеет приоритет по отношению к входу синхросигнала. На языке VHDL модель блока, отображающая поведение триггера-защелки, имеет вид:
D_LATCH: block (CLK = '1' or CLR = '1')
begin
Q <= guarded '0' when CLR = '1'; else
D when CLK = '1'; else
Q;
end block D_LATCH;
В языке VHDL заголовок блока "blоск (СLК = '1' ог СLR = '1')" обозна-чает, что "СLК = '1' ог СLR='1' есть охранное выражение. Под-разумевается, что охранное выражение имеет тип BOOLEAN. Оператор охраняемой конструкции будет выполняться, когда охранное выражение есть истина и сигнал правой части охраняемого оператора меняется или когда охранное выражение меняет свое значение из ложного в истинное. Когда охранное выражение есть ложь, сигнал, указанный в левой части, сохраняет свое прежнее значение. Для приведенного выше примера предположим, что СLR есть О , когда СLK есть 1 , и выход Q будет следовать за входом D. Когда СLК переключится в низкий уровень, зафиксируется последнее значение Q. Таким образом реализуется по-ведение триггера-защелки. Отметим, что функция сброса будет ак-тивироваться, когда СLR = 1, т.е. она является асинхронной.
В противоположность триггеру-защелке, который чувствителен к уровню синхросигнала, многие тактированные триггеры срабатывают по фронту сигнала (ЕDGE__TRIGGERED). Ниже приведено описание на языке VHDL для триггера типа D в варианте со срабатыванием по фронту:
EDGE_TRIGGERED_D: block ((CLK = '1' and not CLK'STABLE)
or CLR = '1')
begin
Q <= guarded '0' when CLR = 1; else
D when CLK = '1' and not CLK'STABLE else
Q;
end block EDGE_TRIGGERED_D;
Отметим, что охранное выражение теперь имеет вид:
(CLK ='1' and not CLK'STABLE) or CLR ='1') .
'STABLE-это атрибут сигнала СLK. Как мы обсуждали в гл. 2, для сигнала X значение Х'STABLE(Т) будет ТRUE, если и только если X сохраняет стабильный уровень в течение последних Т наносекунд. Х'SRABLE(О), который для краткости пишется Х'STABLEЕ, будет FALSE, если и только если значение X только что изменилось. Таким образом, если предположить, что СLR = '0', охранное выражение примет значение ТRUE, как только на входе синхросигнала произойдет переключение из О в 1.
Представление при помощи конечного автомата
Разработчики часто используют для последовательностной схемы представление при помощи конечного автомата. В качестве примера такого представления мы рассмотрим модель конечного автомата, подготовленную Майклом Блау, студентом класса моделирования на уровне СБИС в Технологическом институте шт. Вирджиния. На рис. 3.10 показана диаграмма состояний для автомата Мили с тремя состоя-ниями, который выдает значение 1, когда последние два входных сигнала равны. Описание на языке VHDL для этого автомата приведено на рис. 3.11. Представление автомата Мили подразумевает синхронную схему, поэтому мы используем охраняемые блоки.
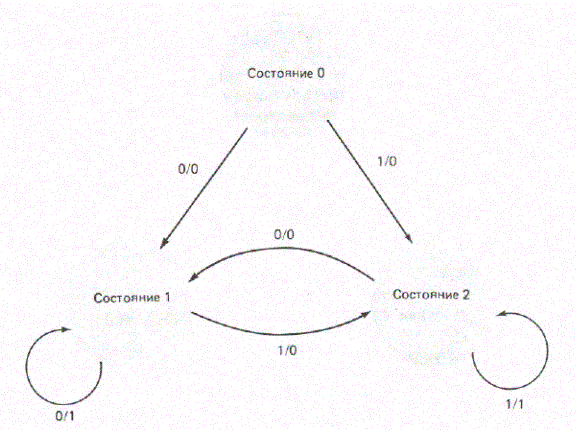
рис. 3.10 Пример автомата Мили

рис. 3.11 Описание автомата Мили на языке VHDL
Для внешнего блока (В1) охранное выражение имеет значение ТRUE, когда синхросигнал CLОСК переключается из 0 в 1. Охранное выражение для внутренних блоков (S0, S1, S2) есть результат логической операции И для текущего состояния и охранного условия внешнего блока. Для представления трех состояний автомата используется перечислимый тип SТАТЕ. Переклю-чение автомата Мили из состояния в состояние представляется при помогли охраняемых условных операторов назначения сигналов в бло-ках S0, S1 и S2. Состояние автомата запоминается в сигнале SТАТЕ _ REG, которым управляют три оператора назначения сигна-лов. В связи с этим здесь требуется функция разрешения шины. Эта функция, SТАТЕ __ RES _ FUNС, описывается в начале блока В1. От-метим, что сигнал SТАТЕ _REG указывается как регистр. Это озна-чает, что драйвер охраняемого оператора назначения, управляющего этим сигналом, будет игнорироваться функцией разрешения шины, когда условие охраны для этого оператора будет ложным. Поскольку в этом случае будут игнорироваться все драйверы, кроме одного, функция разрешения шины выбирает этот активный драйвер и использует его значение как выход функции. Более подробно эту концепцию мы обсудим в гл. 5.
Использование конструкции WAIT
В цифровых системах логический процесс будет часто приостанавли-ваться в своем выполнении, ожидая истечения некоторого периода времени или наступления некоторого события. После истечения ука-занного периода времени или наступления ожидаемого события вы-полнение процесса возобновляется. Эта ситуация может быть про-иллюстрирована следующим образом:
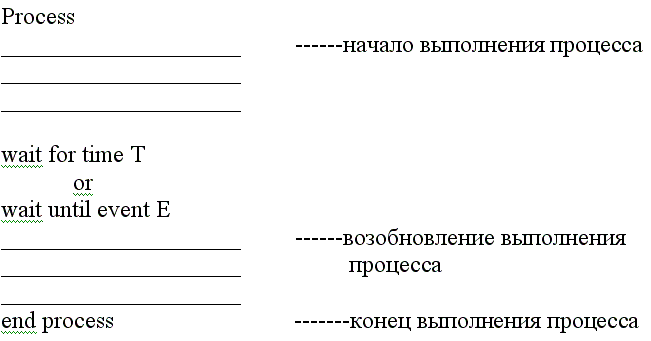
Хотя это может показаться неочевидным, использование механизма ожидания подразумевает поведение последовательностной логики. Что-бы находиться в состоянии ожидания до истечения тайм-аута или появления события, необходимо уметь запоминать состояние и со-хранять последовательность логики. Если возобновление процесса осу-ществляется по истечении тайм-аута, подразумевается наличие счетчика, еще одной последовательностной схемы. Наконец, поскольку процео должен возобновлять свое выполнение после окончания периода ожида ния с того состояния, в котором он находился до этого (в про тивоположность перезапуску), необходимо это предыдущее состояни! процесса сохранять. Это состояние содержит указатель на последующие действия, подлежащие выполнению.
В языке VHDL конструкция ожидания имеет вид:
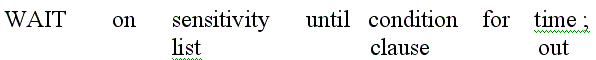
Указанный оператор приостанавливает процесс до момента, пока нe изменится некоторый сигнал в списке чувствительности (сигналов за пуска) процесса (sensitivity list); в эго время будет произведено вы числение условия (condition). Фраза условия есть выражение типa BOOLEAN. Если получается истинное значение, выполнение процесс; возобновляется. Фраза тайм-аута (time out) устанавливает максимальноe время ожидания, после которого процесс возобновит свое выполнение
Пример:
WAIT on X, Y until (Z = 0) for 100 ns.
Этот оператор приостановит процесс до момента изменения X или Y после этого будет проверено выражение Z = 0, и, если результатjv проверки будет истина, процесс возобновится. Но независимо от эти; условий возобновление выполнения процесса произойдет через 100 не
Оператор ожидания WAIT может содержать одно или более условий например, допустимы такие операторы ожидания:
Пример 1: WAIT on X, Y;
Пример 2: WAIT until (Z = 0);
Пример 3: WAIT for 100 ns.
В примере 1 предполагается, что условие имеет всегда истинно значение, так что процесс будег возобновляться, когда изменится X ил У. В примере 2 нет списка сигналов запуска процесса, поэтом; предполагается, что этот список представляется переменной, указанной в условии (т.е. процесс будет возобновляться, когда 2 изменит сво значение из 1 в 0). В примере 3 процесс будет возобновляться чере 100 не независимо от любых других условий.
Следует заметить, что в языке VHDL имеется одно ограничени использования оператора WAIT. В этом языке существуют два вариант оператора-процесса:

Вариант А-это процесс, который активируется, когда меняет свое значение некоторый сигнал в его списке сигналов запуска. Вариант В не имеет списка сигналов запуска и предполагает, что процесс всегда активен. Вариант А фактически эквивалентен следующему:

После начала моделирования процесс выполняется один раз, а затем переходит в состояние ожидания (в конце выполнения), пока не из-менятся сигналы, которые его перезапустят. Для разработчика модели ограничение процесса варианта А заключается в том, что он не может использовать здесь операторы WAIT, поскольку они всегда выполня-лись бы до подразумеваемого оператора WAIT в конце процесса, т.е. был бы потерян смысл процесса варианта А. В то же время, поскольку процессы варианта В могут иметь любое необходимое число операторов WAIT, это по существу не является серьезным ограничением для моделирования.
Существуют две основные области применения конструкции ожи-дания WAIT при моделировании-это моделирование взаимодействия между компонентами и моделирование поведения генератора. Приведем вначале пример моделирования взаимодействия между компонентами:

В приведенном примере процесс INTERFACE всегда активен, однако ждет изменения сигнала А, чтобы начать свое первое действие, которое заключается в формировании сигналов управления интерфейсом. Затем он ждет, чтобы сигнал В переключился из 0 в 1 или истечения тайм-аута, прежде чем начать действовать в зависимости от реакции.
Проиллюстрируем теперь моделирование генератора при помощи конструкции ожидания WAIT:
process
begin
for I in 1 to CLK
CLK<= transport '1' after CLK_PER!OD/2;
CLK <= transport '0' after CLK_PER!OD;
wait for CLK_PERIOD;
end loop;
end process;
Отметим, что показанный процесс продолжает генерировагь синхро-сигналы до тех пор, пока не дойдет до точки NUM_CLK. Однако большую часть своего времени этот процесс проводит в состоянии ожидания.
Первоначально конструкция ожидания была разработана для мо-делирования ЭВМ на архитектурном уровне. Поэтому она не имеет четко определенного аппаратного соответствия. Если вводимое опи-сание предназначается не просто для моделирования поведения за-ведомо работоспособной схемы, а для моделирования с учетом не-исправностей или, быть может, для кремниевой компиляции, разра-ботчику модели, по-видимому, лучше воспользоваться описанием более низкого уровня.
Краткое содержание главы 3
В настоящей главе мы описали базовые методы моделирования цифровой аппаратуры. Важным понятием этого процесса моделирова-ния является параллельное выполнение, отображающее параллельное прохождение сигналов. Мы представили две концепции задержек: дель-та-задержки и временной задержки; обсудили различные подходы к моделированию комбинационных и последовательностных схем на раз-ных уровнях абстракции; показали, что при помощи конструкции ожи-дания WAIT можно моделировать работу последовательностных схем. Методы, описанные в настоящей главе, будут применяться для моде-лирования элементов структур уровня СБИС в остальных главах книги.
Литература
Hill, Frederick J. and Gerald R. Peterson, Introduction to Switching Theory & Logical Design, 3rd Ed., New York: John Wiley & Sons, Inc., 1981.
"VHDL Language Reference Manual, Draft Standard 1076/B," April 1987, CAD Lan-guage Systems, Inc.
"VHDL Tutorial for IEEE Standard 1076 VHDL," June 1987, CAD Language Systems, Inc.
"VHDL User's Manual, Volume 1: Tutorial," August 1985, Intermetrics Inc.